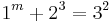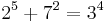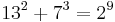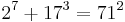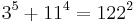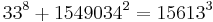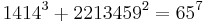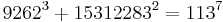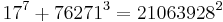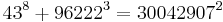Fermat–Catalan conjecture

In number theory, the Fermat–Catalan conjecture combines ideas of Fermat's last theorem and the Catalan conjecture, hence the name. The conjecture states that the equation

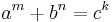
$a^m %2B b^n = c^k\quad$

(Eq.1)

has only finitely many solutions (a,b,c,m,n,k); here a, b, c are positive coprime integers and m, n, k are positive integers satisfying

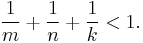
$\frac{1}{m}%2B\frac{1}{n}%2B\frac{1}{k}<1.$

(Eq.2)

As of 2008, the following solutions to Eq.1 are known:^[1]

$1^m%2B2^3=3^2\;$

$2^5%2B7^2=3^4\;$

$13^2%2B7^3=2^9\;$

$2^7%2B17^3=71^2\;$

$3^5%2B11^4=122^2\;$

$33^8%2B1549034^2=15613^3\;$

$1414^3%2B2213459^2=65^7\;$

$9262^3%2B15312283^2=113^7\;$

$17^7%2B76271^3=21063928^2\;$

$43^8%2B96222^3=30042907^2\;$

The first of these (1^m+2³=3²) is the only solution where one of a, b or c is 1; this is the Catalan conjecture, proven in 2002 by Preda Mihăilescu. Technically, this case leads infinitely many solutions of Eq.1 (since we can pick any m for m>6), but for the purposes of the statement of the Fermat-Catalan conjecture we count all these solutions as one.

It is known by Faltings' theorem that for any fixed choice of positive integers m, n and k satisfying Eq.2, only finitely many coprime triples (a, b, c) solving Eq.1 exist, but of course the full Fermat–Catalan conjecture is a much stronger statement.

The abc conjecture implies the Fermat–Catalan conjecture.^[1]

References

^ ^a ^b Pomerance, Carl (2008), "Computational Number Theory", in Gowers, Timothy; Barrow-Green, June; Leader, Imre, The Princeton Companion to Mathematics, Princeton University Press, pp. 361–362, ISBN 9780691118802 .